Isospin-flip excitations in molecules

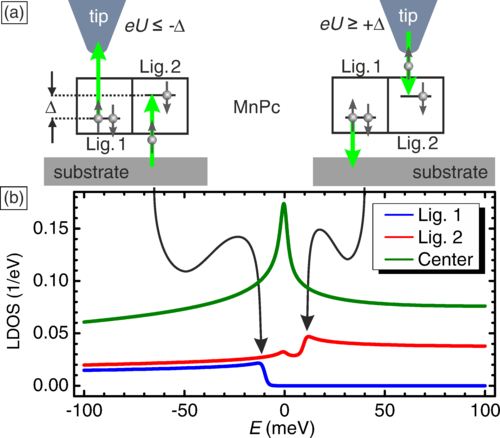
Figure 1. The manganese phthalocyanine (MnPc) shows two orbitals in the ligands of the molecule with an energy difference Δ of ~10 meV. Depending on whether an electron is extracted (negative bias, eU<0) or injected (positive bias, eU>0), an inelastic step appears in the differential conductance signature above one or the other ligand orbital.

Spin-flip excitations are magnetic excitations that are rendered possible by the flipping of spin of a tunneling electron. However, there are other symmetries in molecules that behave like a spin. One of them is orbital degeneracies. If the degeneracy is perfect (totally equivalent orbitals) and an electron from the holding substrate can undistinguishably populate any of the two orbitals, orbital fluctuations driven by the intramolecular Coulomb repulsion can take place. Taking one electron in one of the orbitals is possible because of the coupling to the substrate, but a second electron repels from the first one, and the total energy is too high. This is one type of dynamical correlation. In the presence of an orbital degeneracy, it gives rise to the orbital Kondo effect.

But imagine we have a small Jahn-Teller effect. Then the orbital degeneracy can be lifted. In the case of magnanese phthalocyanines, the Jahn-Teller effect lifts the orbital degeneracy by some 10 meV. Then flipping the orbital needs 10 meV and the orbital Kondo effect is not possible anymore. But injecting electrons above 10 meV may be possible to flip the orbital. This has been shown on the present work. Confirmation of this comes thanks to the spatial resolution of the STM. The STM can inject a 10-meV electron in one of the orbitals or the other depending where it is. As a consequence, the inelastic process (the opening of a new channel when the orbital becomes available) has spatial resolution connected with the sign of the bias.