PhD Thesis Defense | Josu Diego López
 Anharmonic effects in two-dimensional systems: charge density wave transitions and their mechanical stability
Anharmonic effects in two-dimensional systems: charge density wave transitions and their mechanical stability
December 5, 11:00
CFM Auditorium
Candidate: Josu Diego López
Supervisors: Ion Errea and Raffaello Bianco
Summary
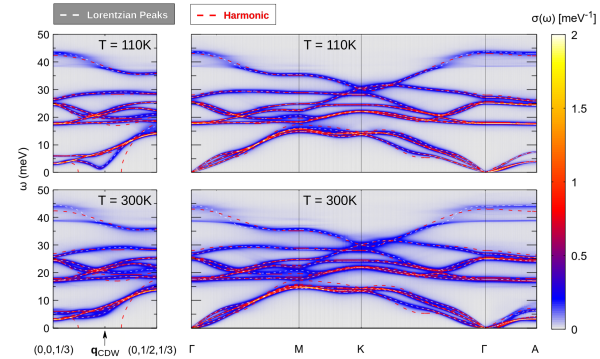
Anharmonic phonon spectral functions for 1T-VSe2 at 110 K and 300 K along (0, k, 1/3) r.l.u and Γ − M − K − Γ − A paths, compared calculations using the harmonic approximation (red dashed lines). The figure illustrates that the main anharmonic renormalization of the phonon frequency concentrates around qCDW.
This thesis focuses on the analysis of non-perturbative anharmonic effects on the ionic dynamics of various physical systems, using the self-consistent harmonic approximation as the main method. Throughout the work, low-dimensional systems are examined, particularly two-dimensional and quasi-two-dimensional materials.
The first part is devoted to the prediction and understanding of charge density wave (CDW) instabilities in transition metal dichalcogenides through first-principles calculations. Specifically, the study focuses on the case of 1T-VSe2, exploring the transition to the charge modulated state both in the bulk structure and in the monolayer. In the bulk case, the analysis successfully combines theoretical results with experimental data obtained by means of inelastic x-ray scattering (IXS) measurements [1, 2]. On the other hand, our theoretical study in the monolayer resolves the longstanding experimental controversy regarding the diverse CDW orders reported in previous studies [3].
In the second part, the mechanical stability of strictly two-dimensional materials is analysed, discussing how thermal fluctuations and anharmonic effects influence their behaviour. This section challenges previous theories about the rigidity of 2D materials, demonstrating that considering anharmonic effects provides a renewed understanding of their mechanical properties [4]. Therefore, the importance of a non-perturbative approach to understanding the stability of these systems is highlighted.
References:
[1] Josu Diego et al. Nature Communications 12, 598 (2021).
[2] Josu Diego et al. Physical Review B 109, 035133 (2024).
[3] Adolfo O. Fumega, Josu Diego, Víctor Pardo, S. Blanco & Ion Errea. Nano Letters 23, 1794 (2023).
[4] Unai Aseginolaza* , Josu Diego* , Tommaso Cea, Raffaello Bianco, Lorenzo Monacelli, Francesco Libbi, Matteo Calandra, Aitor Bergara, Francesco Mauri, and Ion Errea. Nature Physics 20, 1288 (2024).


 Anharmonic effects in two-dimensional systems: charge density wave transitions and their mechanical stability
Anharmonic effects in two-dimensional systems: charge density wave transitions and their mechanical stability