Moiré dispersion of edge states in spin chains on superconductors

Majorana bound states have been predicted at the edge of spin chains on s-wave superconductors. Recent experiments show zero-energy edge states that could be Majorana bound states but they turn out to depend on the spin chain size, leading to strange energy oscillations with the length of the spin chain. This work shows that they are indeed Majorana bound states that are mixed with other in-gap states due to finite size effects. The behavior of the energy originates in the electronic oscillations as contain in the Fermi wave length and in the spin chain periodicity, leading to a moiré pattern that translates into energy oscillations of the lower-energy edge states.

Recent experimental work by Schneider et al. 1 has revealed the appearance of oscillations in the energy of topological edge states due to finite size effects. As the size of the spin chain at the origin of the in-gap states changes, the energy of the edge states also changes. This behavior takes place even when the in-gaps states are in a topological phase where they should be robust zero-energy modes. Moreover, the evolution of the oscillations with the system’s parameters is very strong and at first sight impossible to predict.

Mier et al. show that this is because two competing spatial frequencies produce a moiré pattern. The moiré is produced by the rapid Friedel-like oscillations due to the spin chain on the superconductor, overlaid by the discreteness of the spin lattice. These two periodicities joined in the complicated way of a moiré leading to the above startling behavior. After this realization, it is simple to predict the periodicity of the ensuing oscillations and to design new spin chains. Indeed, the authors propose a special spin chain for the experimental case mentioned before1 that shows no oscillations whatsoever.

Thus, this work combines the recent topic of moiré bands with the novelty that these also happen in classical s-wave superconductors. This work yields a precise explanation of the very-recent experiments of Schneider et al., and the prediction that Mier et al. can design edge states with flat dispersion. Thus topological edge states can be studied independently of the foreseeable size distribution of any procedure to fabricate spin chains.

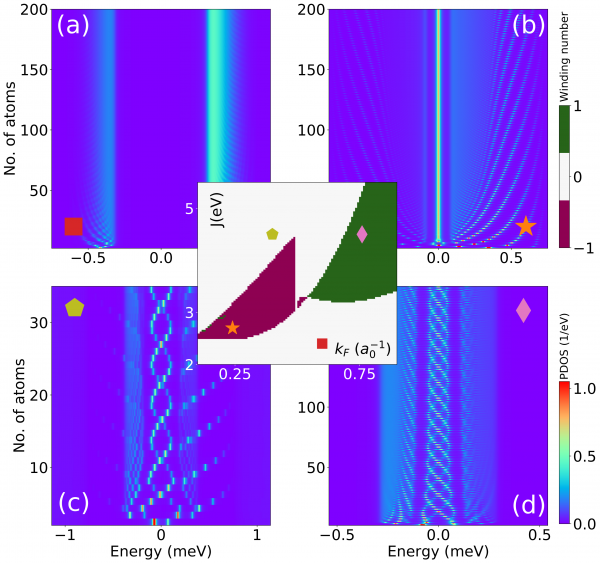
Figure. Four different behaviors of in-gap states as a function of state energy (x-axis) and spin-chain length (y-axis). The four panels correlate with four different phases in the phase diagram of the inset, where the x-axis is the Fermi wave vector (representative of the superconductor´s electronic density) and the y-axis is the Kondo exchange interaction between the spins and the superconductor’s electrons. Red corresponds to a topological phase of widning number +1 and green to winding number -1. The authors show that only for the low density topological region, the Majorana bound states are preserved (b)