Rotational symmetry influences the mechanical properties of graphene

The quantum Theory of Materials group at CFM

Understanding why 2D materials are stable remains in some ways unsolved.  This paper, lead by the quantum Theory of Materials group at CFM, brings together various factors that are important — symmetry and anharmonicity — and combines them to propose a resolution to this long-standing puzzle

Rotational symmetry is shown to protect the quadratic dispersion of out-of-plane flexural vibrations in graphene and other two-dimensional materials against phonon–phonon interactions, making the bending rigidity of these materials non-divergent. The quadratic dispersion is then consistent with the propagation of sound in the graphene plane.

The problem

Many of the applications of graphene rely on its uneven stiffness and high thermal conductivity, and yet its mechanical properties are far from understood. The problem is that standard theories for vibrational properties, such as the harmonic approximation, predict that the flexural vibrational mode has a quadratic dispersion, which yields the unphysical result that in-plane acoustic waves cannot propagate sound1. The quadratic dispersion has thus been questioned, and it has been argued that anharmonic phonon–phonon interactions linearize it.

Even though this correction can explain why sound propagates, it also implies that the bending rigidity of graphene diverges and becomes dependent on the sample size2 — a rather anomalous result. And these problems are not limited to graphene: they are present in all strictly two-dimensional systems, and raise a big question mark over our understanding of their mechanical properties.

The solution

It is symmetry that imposes a quadratic dispersion for the flexural modes in the harmonic approximation: the mode energies are calculated from second derivatives of a potential that is invariant upon rotation, leading to quadratic behaviour in strictly two-dimensional materials. As we have now demonstrated, anharmonic phonons also come from second derivatives of the full free energy of the system, which incorporates phonon–phonon interactions and is also rotationally invariant — implying a quadratic dispersion for the flexural modes, too. We verified this hypothesis by calculating the phonon frequencies of graphene from the second derivatives of the anharmonic free energy both within atomistic simulations and within the membrane models that are widely used in the community working on the physics of flexural modes.

Our results suggest that the anharmonic phonons obtained from the derivatives of the full free energy are indeed quadratic, as imposed by symmetry, despite the presence of phonon–phonon interactions. This proves true in both the atomistic simulations and the membrane model. Remarkably, even if in the harmonic case a quadratic dispersion implies non-propagating sound, within our anharmonic theory this is no longer true because in-plane phonons can propagate sound even if the flexural modes have a quadratic dispersion. One of the main implications of these results is that the bending rigidity is non-divergent at any temperature, overturning the conventional wisdom for two-dimensional membranes that assumed a linearization of the flexural modes and a consequent sample-size-dependent bending stiffness. Another consequence of our results is that the amplitude of the ripples3 in graphene are not suppressed by anharmonicity as previously believed4, but increase with the sample size (Fig. 1).

The implications

Our results offer a consistent, fresh perspective on the mechanical and thermal properties of graphene and indeed all strictly two-dimensional materials. Considering that phonons are at the core of heat transport, our ideas could impact, for instance, the understanding of thermal conductivity in two-dimensional systems.

The results and their implications are, however, limited to intrinsic two-dimensional systems without any external perturbation that breaks rotational symmetry; also to situations in which the average positions of the atoms in the two-dimensional material are strictly in the plane. In practical experiments, two-dimensional materials are generally grown on substrates that exert some strain, even if small, that breaks rotational symmetry. It remains to be seen what the implications of our results would be in these conditions.

It is also not clear that two-dimensional materials are strictly flat — as we have assumed — and do not show static ripples. We have shown, however, that this flat solution is indeed dynamically stable. The next step, to further support the interpretation of the mechanical properties of two-dimensional materials, will be to clarify whether static ripples can be formed in unstrained graphene and whether their formation is or is not energetically favoured within the formalism that we have used in this present work.

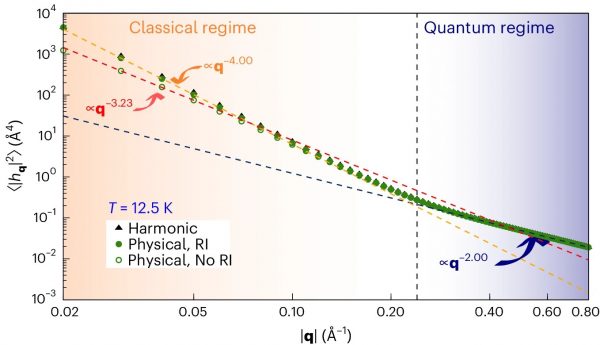
The amplitude of ripples in a membrane are typically studied via the height correlation function in momentum space, 〈|hq|2〉. Here, the height fluctuations of graphene are presented from the Fourier transform of the height–height correlation function, versus the wave number q, at 12.5 K. When there is the full rotational invariance (RI), the physical result scales as q−4 in the classical regime; but the exponent is lower when rotational invariance is broken (no RI). The physical RI results coincides practically with the harmonic solution. Bending rigidity scales as the correlation function times q4 and so diverges in the absence of rotational symmetry, though not when rotational symmetry holds.