A quantum-geometric theory of optical spatial dispersion in crystals

The light-matter interaction is often treated by setting the wave vector q=2π/λ to zero. While this is an excellent approximation for many purposes because λ is typically much larger than atomic dimensions, it fails to capture phenomena such as natural optical activity, the rotation of the plane of polarization of light as it travels through a chiral medium, depicted in the figure.

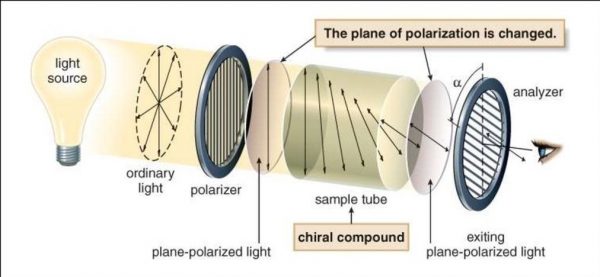
Figure: Optical rotation induced by a chiral medium

Such spatially-dispersive effects originate in the weak spatial inhomogeneity of the electromagnetic field on the atomic scale. In molecules, they are described by the multipole theory of electromagnetism, where the coupling to light is treated by including terms beyond the electric-dipole (or infinite-wavelength) approximation. That theory has two shortcomings: it is limited to bounded systems, and its building blocks – the multipole transition moments – are origin dependent.

In this work, we develop a quantum-geometric theory of optical spatial dispersion in crystals.

Working in the independent-particle approximation, we introduce intrinsic multipole transition moments that are origin independent and transform covariantly under gauge transformations of the Bloch states. Electric-dipole transitions are given by the Berry connection, while magnetic-dipole and electric-quadrupole transitions are described by the intrinsic magnetic moment (spin plus orbital) and by the quantum metric of the Bloch states, respectively. In addition to multipole-like terms, the optical response of crystals at first order in q contains additional terms proportional to the band velocity that have no counterpart in molecular theories.

A neat outcome of this theory is a topological rotatory-strength sum rule. It has been known  since the early days of quantum mechanics that the rotatory strength of chiral molecules (the difference in absorption strength of left- and right-circularly polarized light) sums to zero over all optical transitions. We have found that this sum rule remains valid for optically-active metals for a surprising reason: the rotatory strength integrated over all frequencies is equal to the sum of the Chern numbers of all the Fermi-surface pockets, which in turn must vanish for topological reasons.