Gyrotropic Magnetic Effect and the Magnetic Moment on the Fermi Surface

Optical responses in chiral topological semimetals

One of the characteristic signatures of topological phases is the existence of robust gapless states in the surface band structure. In addition, topological phases that are insulating in the bulk often have quantized bulk electromagnetic responses, such as the integer quantum Hall effect. Gapless phases with topological features, such as Dirac and Weyl semimetals in 3D, can also have interesting electromagnetic responses, although one might not expect them to be quantized. In this work this group found that certain nonmagnetic Weyl semimetals display a peculiar type of magnetoelectric effect: a bulk current is induced by an oscillating magnetic field and, conversely, a bulk magnetization is induced by the passage of a current. This “kinetic magnetoelectric effect” is the low-frequency limit of natural optical activity, and it should be observable in optical rotation on mirror-free Weyl semimetals.  Microscopically, it is determined at low frequency by the magnetic moments of Bloch electrons on the Fermi surface. While the effect is not exclusive to Weyl semimetals, for them it takes a particularly simple form: the rotatory power is proportional to the energy separation between the 3D bulk Dirac cones of opposite chirality.

At present, the group is using first-principles methods to investigate this and related optical phenomena (e.g., the current-induced Faraday rotation) in chiral nonmagnetic conductors such as doped trigonal tellurium. In this material, the Te atoms form helical chains, as depicted in the figure.  The passage of a current along the helical axis then induces a parallel orbital magnetization, i.e., it is as if the helical chains behaved like microscopic solenoids.

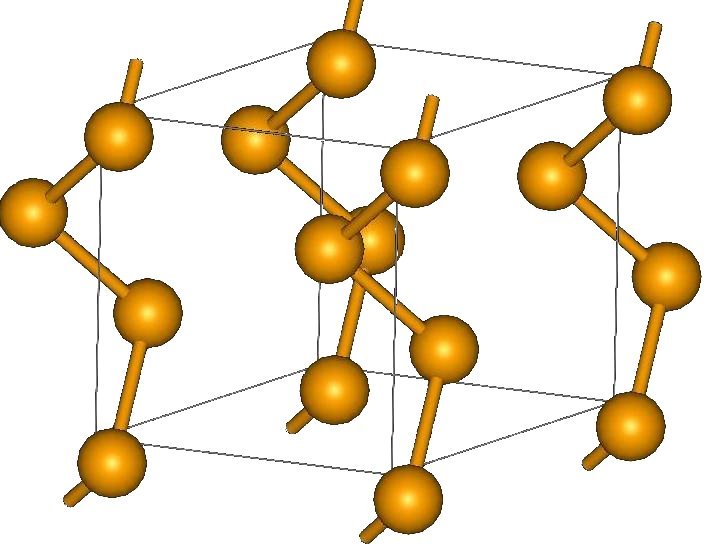
The crystal structure of trigonal tellurium. The tellurium atoms are arranged along helical chains, which can be either right-handed (as shown here) or left handed.