Kerker conditions upon lossless, absorption, and optical gain regimes

A nanoantenna with balanced electric and magnetic dipole moments exhibits a directive radiation pattern with zero backscattering. This is known as the first Kerker condition after Kerker, Wang, and Giles, who predicted in 1983 that, under plane wave illumination, magnetic spheres with equal relative permittivity and permeability radiate no light in the backscattering direction. They also concluded that, for certain permittivity and permeability relations for nanospheres, this zero optical light scattering condition happened in the forward direction.

Three decades later, a renewed version of these ideas was proposed for subwavelength dielectric spheres of high refractive index (HRI) materials, reinvigorating the interest on these light scattering conditions. Interestingly, the scattering properties of HRI nanospheres can be fully described by dipolar modes. At the first Kerker condition the electric and magnetic dipolar modes oscillate in phase with equal amplitude. This optical response drives to destructive interference between the scattered fields at the backscattering direction, which is commonly referred to as the zero optical backscattering condition.

This anomalous light scattering condition was first experimentally measured in the limit of small particle in the microwave regime for ceramic spheres and, soon after, in the visible spectral range for HRI Si and GaAs nanospheres.

However, recent results suggest that the concept of small particle is sufficient, but not necessary, to guarantee a dipolar response in the optical scattering of an object. Consequently, the mentioned backscattering anomalies could also be measured on larger dielectric particles.

The absence of backscattered light emerges at the first Kerker condition for dipolar particles regardless of the incoming polarization. On the other hand, for cylindrically symmetric particles, the absence of backscattered light follows from the preservation of electromagnetic helicity. Conservation of helicity has proven crucial in many applications such as enhanced chiral light-matter interactions, or in the spin-orbit interactions of light. Remarkably, it has been reported that from a relatively simple far-field measurement of the electromagnetic helicity at a right angle, the radiation pattern of the dipolar particle is inferable.

Now, a team of researchers analytically demonstrates that either losses or optical gain inhibit the first Kerker condition for homogeneous spheres regardless of the particle’s size, incident wavelength, incoming polarization, and multipole order. It follows that dissipating spheres such as dielectric Mie spheres in the visible spectral range and plasmonic particles, such as metal spheres, cannot exhibit the first Kerker condition.

For a germanium (Ge) sphere in the dipolar regime, the team quantifies the gradual drift from the ideal zero optical backscattering condition as the absorption rate is increased. Finally, that optical gain is mandatory to reach the zero forward light scattering condition is demonstrated.

The researchers show that the electromagnetic helicity cannot be preserved after scattering by an arbitrary dielectric sphere in the presence of losses or optical gain. Hence, neither can the zero optical backscattering condition be fulfilled in that scenario.

These results unveil a hidden connection between two symmetries from fundamental principles: energy conservation, mathematically expressed in terms of the optical theorem, and the electromagnetic duality, which is restored at the first Kerker condition. This intriguing link opens new insights into Mie theory.

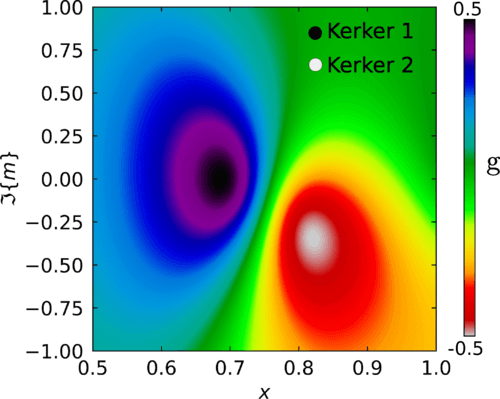
Figure: (a) Real (dash-dotted red) and imaginary part (dashed-red) of the refractive index contrast (m) vs the incident wavelength (λ) for a Ge sphere. Maximum of the expected value of the EM helicity in solid blue, ⟨Λ⟩max, for a Ge sphere vs λ under plane wave illumination with σ=+1. (b) Color map of ⟨Λ⟩ vs λ and particle’s size (R) for a Ge sphere under plane wave illumination with σ=+1. The visible range is encompassed by a dashed rectangle. As mentioned in the text, in this region helicity conservation is never fulfilled.