Mirror Chern numbers in the hybrid Wannier representation

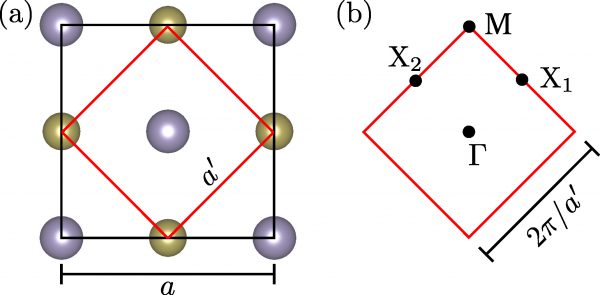
Figure 1: (a) Atomic structure of monolayer SnTe. The black square is the conventional unit cell with lattice constant a, and the red square is the primitive cell with lattice constant a’ = a/√2.
(b) Brillouin zone and high-symmetry points.

Electron in crystals are usually described in terms of extended Bloch states. An alternative representation is in terms of localized Wannier orbitals. Here, Rauch et al. use an intermediate “hybrid Wannier representation”, where states are localized in one spatial direction and extended in the other directions, to study topological properties.

The topology of electronic states in band insulators with mirror symmetry can be classified in two different ways. One is in terms of the mirror Chern number, an integer that counts the number of protected Dirac cones in the Brillouin zone of high-symmetry surfaces. The other is via a Z₂ index that distinguishes between systems that have a nonzero quantized orbital magnetoelectric coupling (“axion-odd”) and those that do not (“axion-even”); this classification can also be induced by other symmetries in the magnetic point group, including time reversal and inversion. A systematic characterization of the axion Z₂ topology has previously been obtained by representing the valence states in terms of hybrid Wannier functions localized along one chosen crystallographic direction and inspecting the associated Wannier band structure.

Here, the researchers focus on mirror symmetry, and extend that characterization to the mirror Chern number. The authors choose the direction orthogonal to the mirror plane as the Wannierization direction and show that the mirror Chern number can be determined from the winding numbers of the touching points between Wannier bands on mirror-invariant planes and from the Chern numbers of flat bands pinned to those planes. In this representation, the relation between the mirror Chern number and the axion Z₂ index is readily established. The formalism is illustrated by means of ab initio calculations for SnTe in the monolayer and bulk forms, complemented by tight-binding calculations.

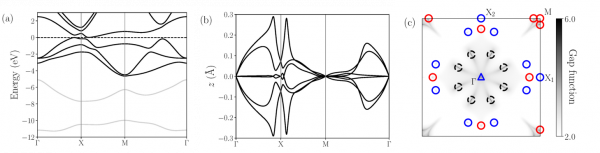
Figure 2: (a) Doubly-degenerate energy bands of monolayer SnTe, with the s-type lower valence bands that are excluded from the Wannierization shown in gray. (b) Wannier bands obtained from the Bloch states in the six p-type upper valence bands. (c) Heat map plot of the gap function for the central pair of Wannier bands, where zero-gap points (nodal points) appear as dark spots. Those with winding numbers Wj = ±1 are indicated by red or blue circles, while the one with Wj = −3 at the Г point is indicated by a blue triangle. Dashed circles denote pairs of nearby nodes with equal and opposite winding numbers. The mirror Chern number, given by the sum of the winding numbers divided by two, is -2. Thus, monolayer SnTe is a topological crystalline insulator.